Lab 2
Get the code
Find the Lab 2 code in the class repository.
$ ls
README.md classes/ labs/ scripts/
$ ls labs/lab2
README cpp/ julia/ python/ rust/
$ ls labs/lab2/cpp
curves.cpp makefile triples.cpp view-trip.gp
The instructions here focus on C++, but you may carry out the comparable steps in Julia, Python, or Rust. You only need to submit your solutions for a single programming language.
Ordered tuples
The lab2 directory contains a short C++ program named
triples.cpp that outputs all strictly ordered triples of the
integers 0 to 6 (inclusive). The make command invokes the compiler,
which creates an executable named triples.
$ make triples
g++ -o triples triples.cpp -O -ansi -pedantic -Wall
$ ./triples
(0,1,2)
(0,1,3)
(0,2,3)
(1,2,3)
.
.
.
(1,5,6)
(2,5,6)
(3,5,6)
(4,5,6)
Modify the program so that instead it counts the number of such triples. Generalize to integers \(\mathsf{0}, \mathsf{1}, \ldots, \mathsf{N}\), and output the results in two-column format for all values of \(\mathsf{N}\) from 2 to 10. You should be able to reproduce the following.
$ make triples
g++ -o triples triples.cpp -O -ansi -pedantic -Wall
$ ./triples
2 1
3 4
4 10
5 20
6 35
7 56
8 84
9 120
10 165
$ ./triples > trip.dat
$ gnuplot view-trip.gp
(If your plot doesn’t persist, you may have to type
gnuplot -p view-trip.gp. Whether the -p flag is required
depends on which operating system you’re running. Alternatively, you
can add pause -1 as the last line of your gnuplot script.)
Redirection from stdout to a file via > trip.dat is a shell feature
and not specific to C++, which is to say that you can do all of the
following:
$ cd ../julia
$ julia triples.jl > trip.dat
$ cd ../python
$ python3 triples.py > trip.dat
$ cd ../rust
$ rustc triples.rs
$ ./triples > trip.dat
$ cd ../cpp
Using your solution to triples.cpp as a template, create a program
file quadruples.cpp that writes three columns of data:
\(\mathsf{N}\) from 0 to 99, the number of weakly ordered
quadruples \(\mathsf{(i,j,k,l)}\) formed from the integers
\(\mathsf{0}\) through \(\mathsf{N}\), and how many of the sums
\(\mathsf{i^2 + j^2 + k^2 + l^2}\) are perfect squares.
(Strict ordering of \(\mathsf{i}\), \(\mathsf{j}\),
\(\mathsf{k}\), and \(\mathsf{l}\) implies that
\(\mathsf{i < j < k < l}\). Weak ordering implies
that \(\mathsf{i \le j \le k \le l}\).)
$ make quadruples
g++ -o quadruples quadruples.cpp -O -ansi -pedantic -Wall
$ ./quadruples
0 1 1
1 5 3
2 15 6
3 35 8
4 70 14
5 126 18
. . .
. . .
. . .
97 4082925 15689
98 4249575 16213
99 4421275 16462
Determine whether an integer is a perfect square by whatever means. You
may want to use std::sqrt from the cmath library in combination
with integer casting.
Following view-trip.gp, compose a gnuplot script file view-quad.gp
that plots the number of perfect squares alongside the 3rd- and
4th-order polynomial fits to the data.
Selection rules
The hydrogen atom consists of a single electron orbiting a positively charged nucleus. The electron can exist only in discrete orbitals characterized by the radial quantum number \(\mathsf{n} = \mathsf{1}, \mathsf{2}, \mathsf{3}, \ldots\) and the angular momentum quantum numbers \(\mathsf{l} = \mathsf{0}, \mathsf{1}, \mathsf{2}, \ldots, \mathsf{n-1}\) and \(\mathsf{m} = \mathsf{-l}, \ldots, \mathsf{-1}, \mathsf{0}, \mathsf{1}, \ldots, \mathsf{l}\). The energy of each orbital, \(\mathsf{E_n} = \mathsf{-(13.6\,\textsf{eV})/n^2}\), is a function of the radial quantum number alone. Hence, each energy level is \(\mathsf{g_n}\)-fold degenerate, where \(\mathsf{g_n} = \mathsf{\sum_{l=0}^{n-1} (2l+1)} = \mathsf{n^2}\). (In other words, there are \(\mathsf{g_n} = \mathsf{n^2}\) states having the same energy \(\mathsf{E_n}\).)
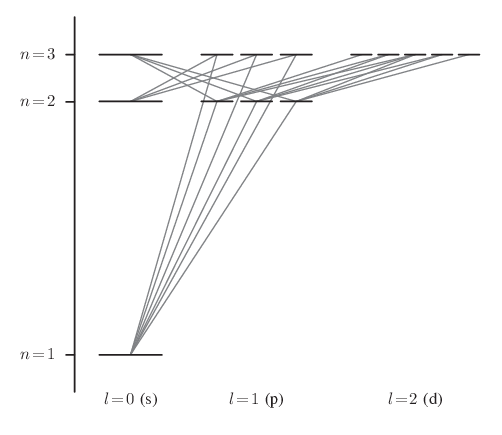
Transitions between orbitals can occur if the electron absorbs or emits a photon. But since a quantum of light has intrinsic angular momentum (1 in units of \(\mathsf{\hbar}\)), conservation laws put a strict limit on which atomic transitions are possible. This leads to the famous electric dipole selection rules: \(\mathsf{\Delta l} = \pm \mathsf{1}\) and \(\mathsf{\Delta m} = \mathsf{0}, \pm \mathsf{1}\). Allowed transitions between the various states with \(\mathsf{n} = \mathsf{1}, \mathsf{2}, \mathsf{3}\) are shown in the following diagram.
Complete the program selection.cpp so that it computes all possible
transitions of the form \(\mathsf{n_2} \to \mathsf{n_1}\) with
\(\mathsf{n_1} < \mathsf{n_2} \le \mathsf{20}\). Have the program
output the results in four columns indicating the initial and final
radial quantum numbers, the number of allowed pathways, the energy of
the emitted photon \(\mathsf{\Delta E} = \mathsf{E_2}
- \mathsf{E_1}\), and its wavelength \(\lambda = \mathsf{hc/\Delta
E}\) in nanometers. (Recall that \(\mathsf{hc}
= \mathsf{1240}\,\textsf{eV}\cdot\textsf{nm}\).)
$ make selection
g++ -o selection selection.cpp -O2 -ansi -pedantic -Wall -lm
$ ./selection | head -n5
2->1 3 10.2 121.569
3->1 3 12.0889 102.574
3->2 15 1.88889 656.471
4->1 3 12.75 97.2549
4->2 15 2.55 486.275
Modify selection.cpp so that the spectral lines in the visible
spectrum, \(\mathsf{380}\,\textsf{nm} < \mathsf{\lambda}
< \mathsf{750}\,\textsf{nm}\), are marked with a lowercase v.
$ make selection
g++ -o selection selection.cpp -O2 -ansi -pedantic -Wall -lm
$ ./selection | head -n5
2->1 3 10.2 121.569
3->1 3 12.0889 102.574
3->2v 15 1.88889 656.471
4->1 3 12.75 97.2549
4->2v 15 2.55 486.275
$ ./selection | grep v
3->2v 15 1.88889 656.471
4->2v 15 2.55 486.275
5->2v 15 2.856 434.174
6->2v 15 3.02222 410.294
7->2v 15 3.12245 397.124
8->2v 15 3.1875 389.02
9->2v 15 3.2321 383.652
Spin sectors
Quantum particles have a property called spin, which is an intrinsic angular momentum. The spin of a particle is restricted to be a multiple of \(\mathsf{\hbar/2}\). In units where \(\mathsf{\hbar} = \mathsf{1}\), the spin is either an integer or an odd multiple of one half. Electrons have spin \(\mathsf{s=1/2}\).
The total spin \(S\) of a collection of electrons is determined by the angular momentum summation rule \(\mathsf{\tfrac{1}{2}} \otimes \mathsf{S} = \mathsf{(S-\tfrac{1}{2})} \oplus \mathsf{(S + \tfrac{1}{2})}\). The possible spin sectors for two, three, and four electrons are shown below.
The final line shows the general result for \(\mathsf{N}\) electrons. The coefficient \(\mathsf{C_S^{(N)}}\) denotes the number of states in a given spin sector. One can show that the total number of states in the singlet (\(\mathsf{S=0}\)) sector is
and that the total number of states—counting the \((\mathsf{2S+1})\)-fold degeracy—is
The \(\mathsf{2^N}\) result is just the number of ways to orient \(\mathsf{N}\) electrons either spin-up or spin-down.
Read over the file moments.cpp. It provides the skeleton of
a program that computes the coefficients \(\mathsf{C_S^{(N)}}\) and
displays them in a table. Determine how elements of the array
current (indexed by the integer \(\mathsf{2S}\)) should be
incremented in terms of the values in last. Accumulate the total
number of states into the variable num_states. The output of your
program should be identical to the following.
$ make moments
g++ -o moments moments.cpp -O2 -ansi -pedantic -Wall -lm
$ ./moments
0 0.5 1 1.5 2 2.5 3 num
+-------------------------------------------------+-------
1| 1 | 2
2| 1 1 | 4
3| 2 1 | 8
4| 2 3 1 | 16
5| 5 4 1 | 32
6| 5 9 5 1 | 64
7| 14 14 6 | 128
8| 14 28 20 7 | 256
9| 42 48 27 | 512
10| 42 90 75 35 | 1024
11| 132 165 110 | 2048
12| 132 297 275 154 | 4096
13| 429 572 429 | 8192
14| 429 1001 1001 637 | 16384
15| 1430 2002 1638 | 32768
16| 1430 3432 3640 2548 | 65536
+-------------------------------------------------+-------
Write a function verify_singlet that computes
\(\mathsf{C_0^{(N)}}\) explicitly. Check its result against
last[0] for each even value of n from 2 to Nmax.