Phys 712 — Spring 2015 — Assignment 1 (Partial Solutions)

  1. …

  2. (a) …

    (b) …

  3. (a) …

    (b) Make a plot of \(P_\uparrow(t)\) with \(t\) running over four complete cycles of the field oscillation. Show example curves for the case of fast (\(\omega_0 \gg J_0/\hbar\)) and slow (\(\omega_0 \gg J_0/\hbar\)) oscillation.

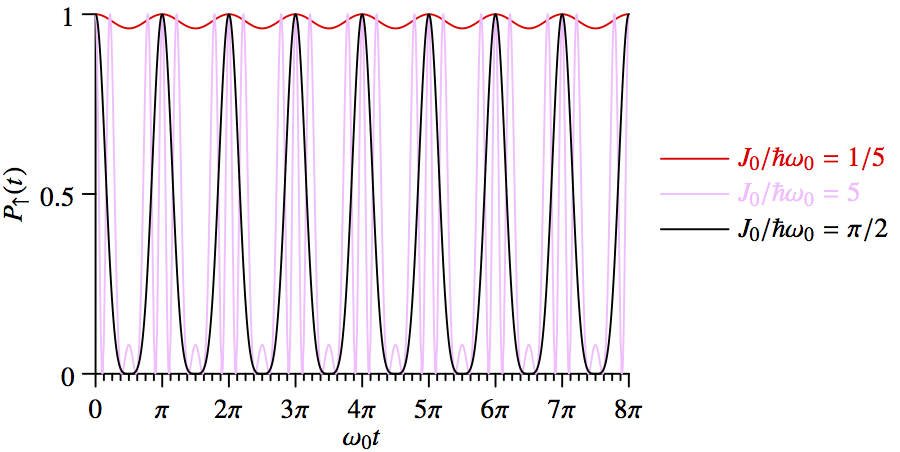
This plot is generated with the following Asymptote code.

import graph;

size(400,200,IgnoreAspect);
defaultpen(0.85);

usepackage("newtxtext,newtxmath");

real a;
real f(real x) { return cos(a*sin(pi*x))**2; }

a=0.2;
draw(graph(f,0,8,1000, operator ..),red, "$J_0/\hbar\omega_0 = 1/5$");
a=5.0;
draw(graph(f,0,8,1000, operator ..),pink, "$J_0/\hbar\omega_0 = 5$");
a = 0.5*pi;
draw(graph(f,0,8,1000, operator ..),black, "$J_0/\hbar\omega_0 = \pi/2$");

string times_pi(real x) { 
   if (fabs(x) < 0.1) return "$0$";
   if (fabs(x-1.0) < 0.1) return "$\pi$"; 
   return "$" + string(x) + "\pi$"; }

xaxis("$\omega_0 t$",Bottom,RightTicks(times_pi,0,8));
yaxis("$P_{\uparrow}(t)$",Left,LeftTicks(0,1));

add(legend(1,3,3,30,0,1.2,0,0,invisible()),point(E),10E,UnFill);