Universal Aspects of Barrier Crossing Under Bias
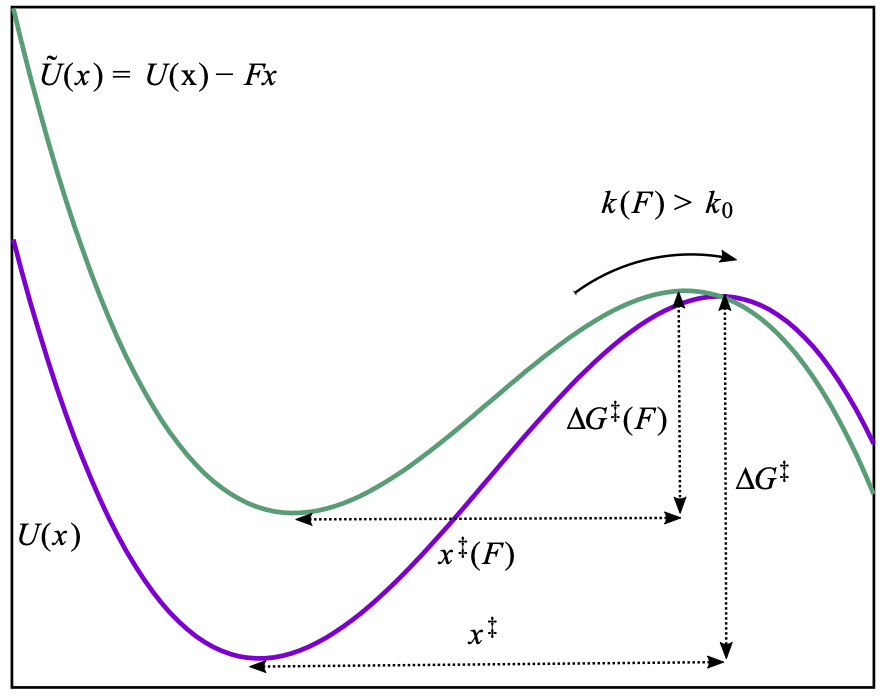
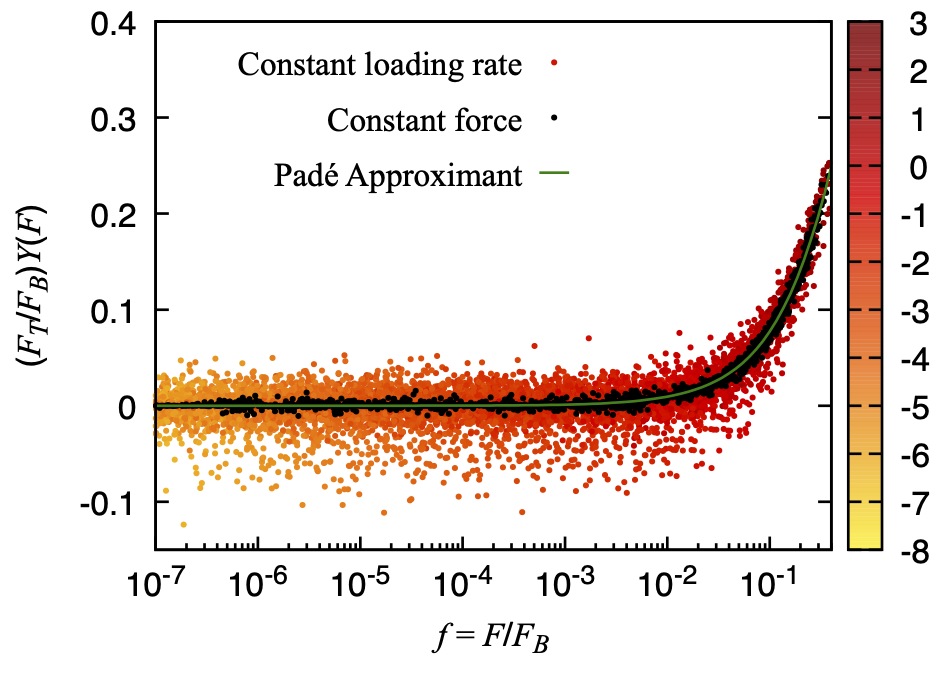
The thermal activation process by which a system passes from one local energy minimum to another is a recurring motif in physics, chemistry, and biology. For instance, biopolymer chains are typically modeled in terms of energy landscapes, with folded and unfolded conformations represented by two distinct wells separated by a barrier. The rate of transfer between wells depends primarily on the height of the barrier, but it also depends on the details of the shape of the landscape along the trajectory. We consider the case of bias due to an external force, analogous to the pulling force applied in optical tweezer experiments on biopolymers. Away from the Arrhenius-law limit and well out of equilibrium, somewhat idiosyncratic behavior might be expected. Instead, we identify universal behavior of the biased activated-barrier-crossing process and demonstrate that data collapse onto a universal curve can be achieved for simulated data over a wide variety of energy landscapes having barriers of different height and shape and for loading rates spanning many orders of magnitude.