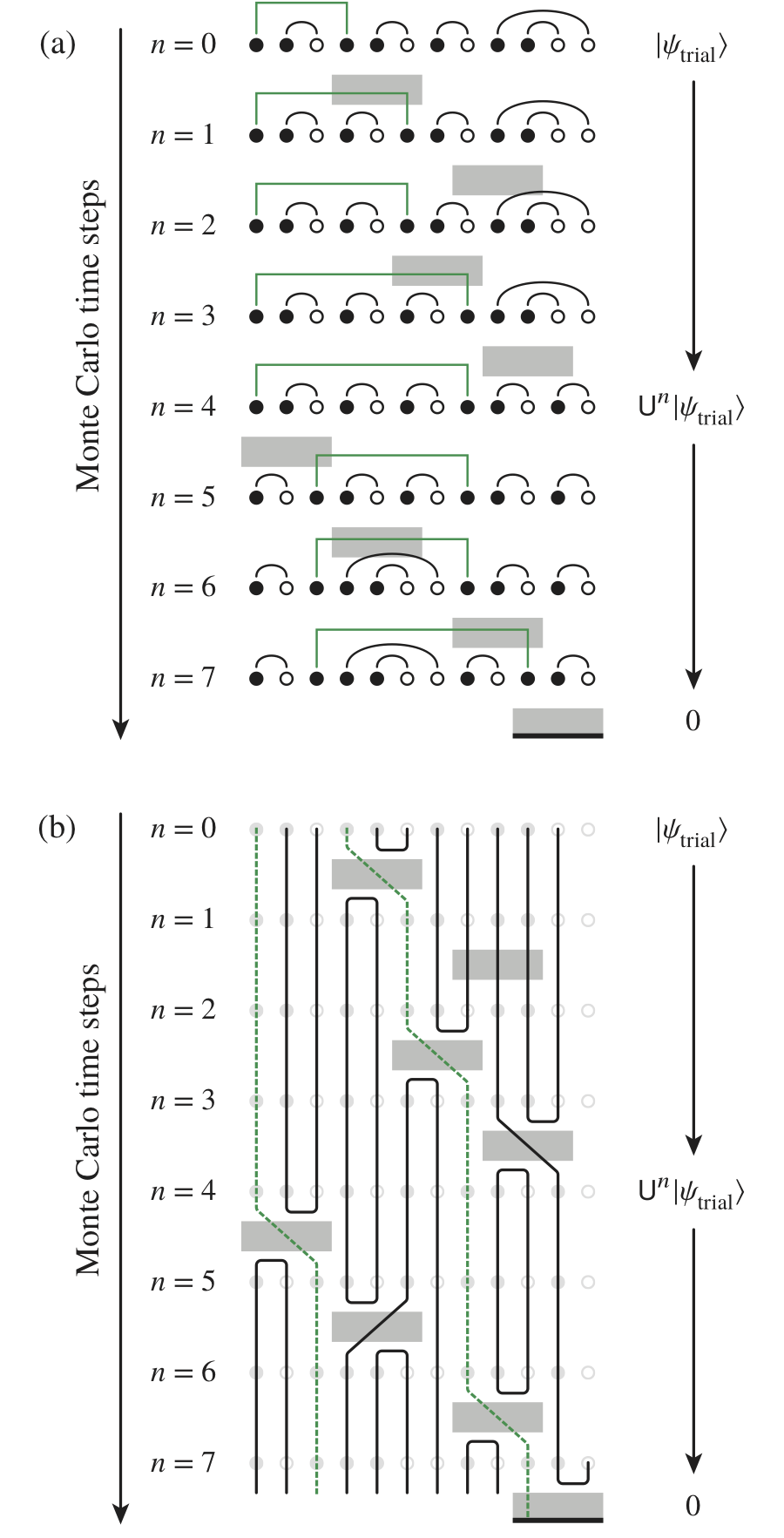
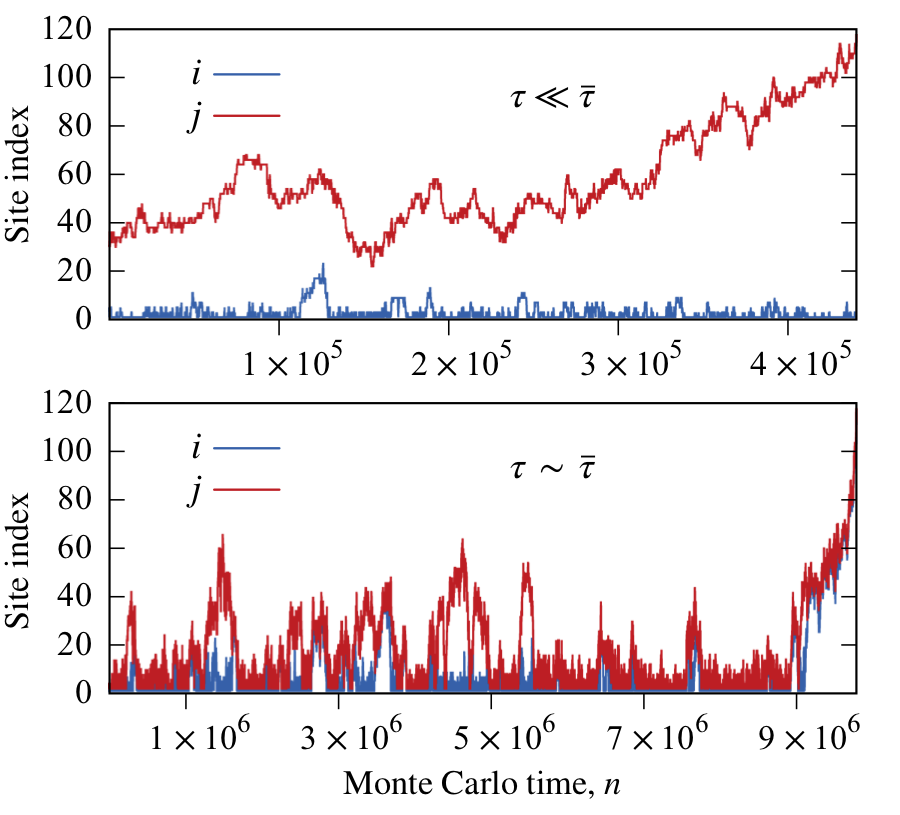
The dynamical behavior of a quantum many-particle system is characterized by the lifetime of its excitations. When the system is perturbed, observables of any non-conserved quantity decay exponentially, but those of a conserved quantity relax to equilibrium with a power law. Such processes are associated with a dynamical exponent z that relates the spread of correlations in space and time. We present numerical results for the Fredkin model, a quantum spin chain with a three-body interaction term, which exhibits an unusually large dynamical exponent. We discuss our efforts to produce a reliable estimate z=3.16(1) through direct simulation of the quantum evolution and to explain the slow dynamics in terms of an excited bond that executes a constrained random walk in Monte Carlo time.

@article{
  title = {Slow dynamics of the Fredkin spin chain},
  author = {Adhikari, Khagendra and Beach, K. S. D.},
  journal = {Physical Review B},
  volume = {104},
  issue = {11},
  pages = {115149},
  numpages = {12},
  year = {2021},
  month = {Sep},
  publisher = {American Physical Society},
  doi = {10.1103/PhysRevB.104.115149},
  url = {https://journals.aps.org/prb/abstract/10.1103/PhysRevB.104.115149}
}