Tunable quantum spin chain with three-body interactions
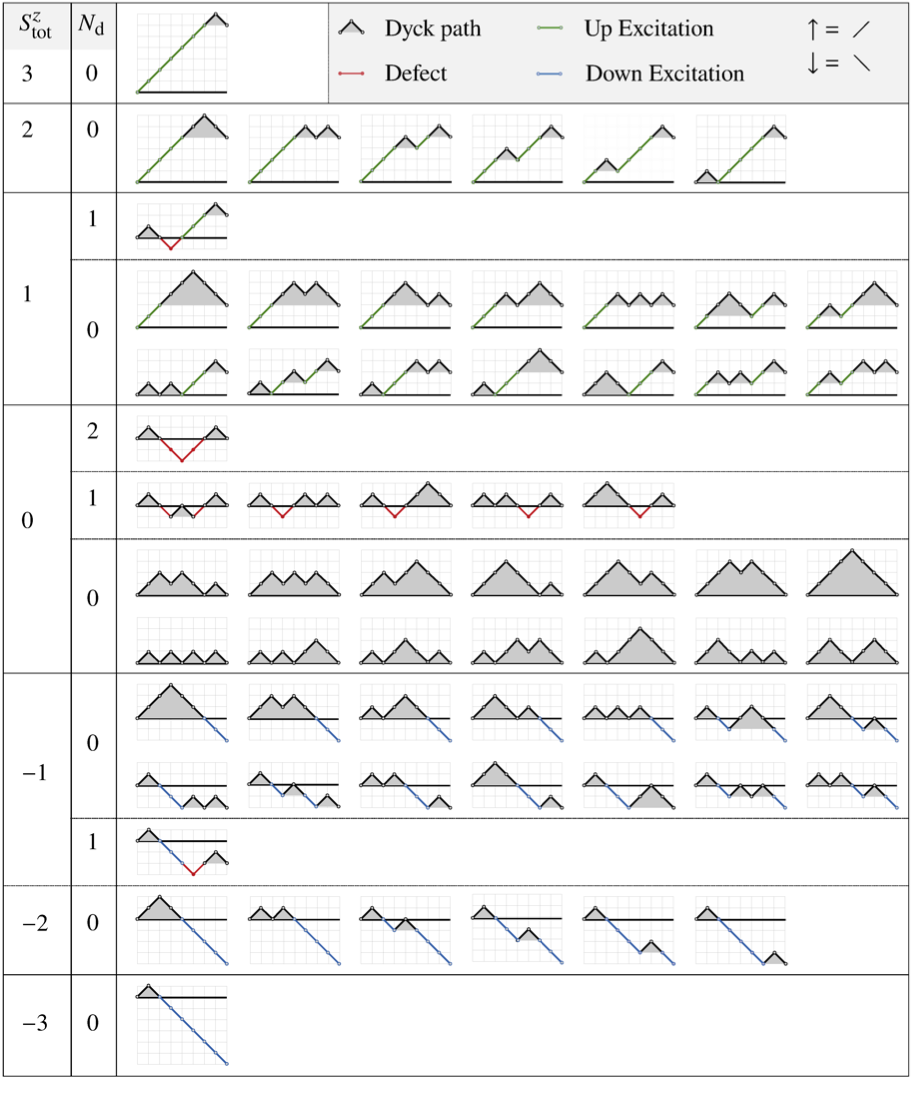
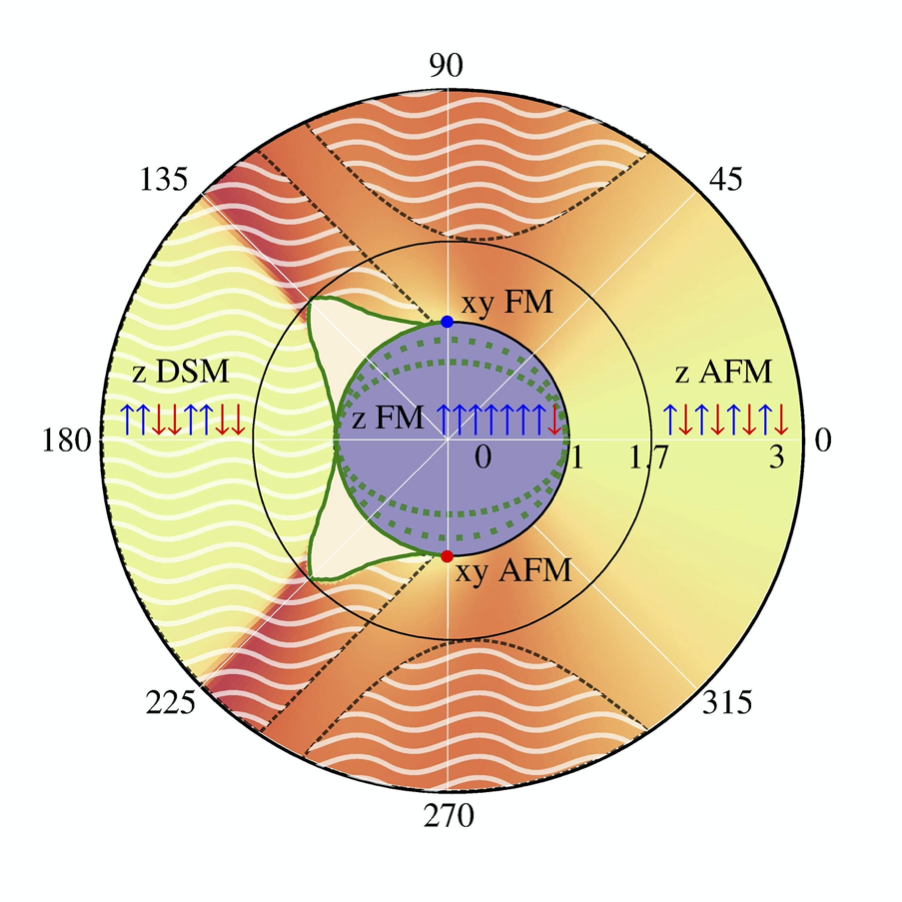
We introduce a generalization of the Fredkin spin chain with tunable three-body interactions expressed in terms of conventional spin-half operators. Of the model’s two free parameters, one controls the preference for Ising antiferromagnetism and the other controls the strength of quantum fluctuations. In this formulation, the so-called t-deformed model (an exactly solvable, frustration-free Hamiltonian) lives on a unit circle centered on the origin of the phase diagram. The circle demarcates the boundary between ferromagnetic order inside and various antiferromagnetic phases outside. Throughout most of the non-ferromagnetic parts of the phase diagram, the ground state has Dyck word form: i.e., all contributing spin configurations exhibit perfect matching and nesting of spin up and spin down. The exceptions are two regions in which Dyck word mismatches are energetically favorable. We remark that in those regions the energy level spacing can be exponentially small in the system size. It is also the case that exact diagonalization reveals a highly idiosyncratic energy spectrum, presumably because the hard spin twist at the chain ends induces strong incommensurability effects on the bulk system when the chain length is small. As a convergence check, we benchmark our DMRG results to near-double-precision floating-point accuracy against analytical results at exactly solvable points and against exact diagonalization results for small system sizes across the entire parameter space.
@article{
title = {Tunable quantum spin chain with three-body interactions},
author = {Adhikari, Khagendra and Beach, K. S. D.},
journal = {Physical Review B},
volume = {102},
issue = {18},
pages = {184415},
numpages = {13},
year = {2020},
month = {Nov},
publisher = {American Physical Society},
doi = {10.1103/PhysRevB.102.184415},
url = {https://journals.aps.org/prb/abstract/10.1103/PhysRevB.102.184415}
}