Deforming the Fredkin spin chain away from its frustration-free point
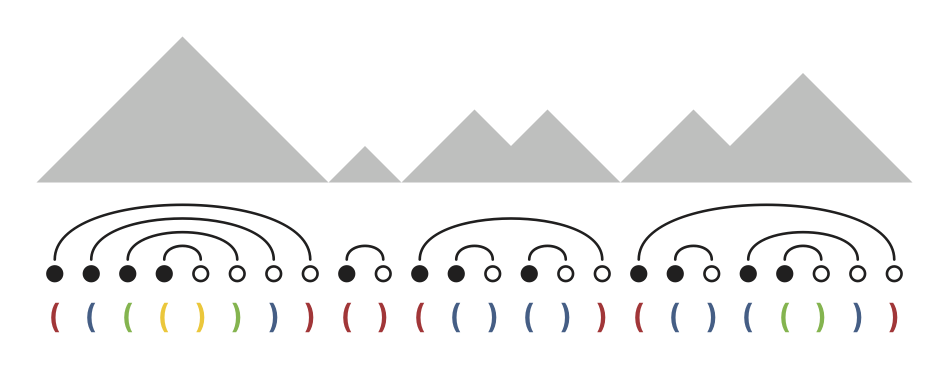
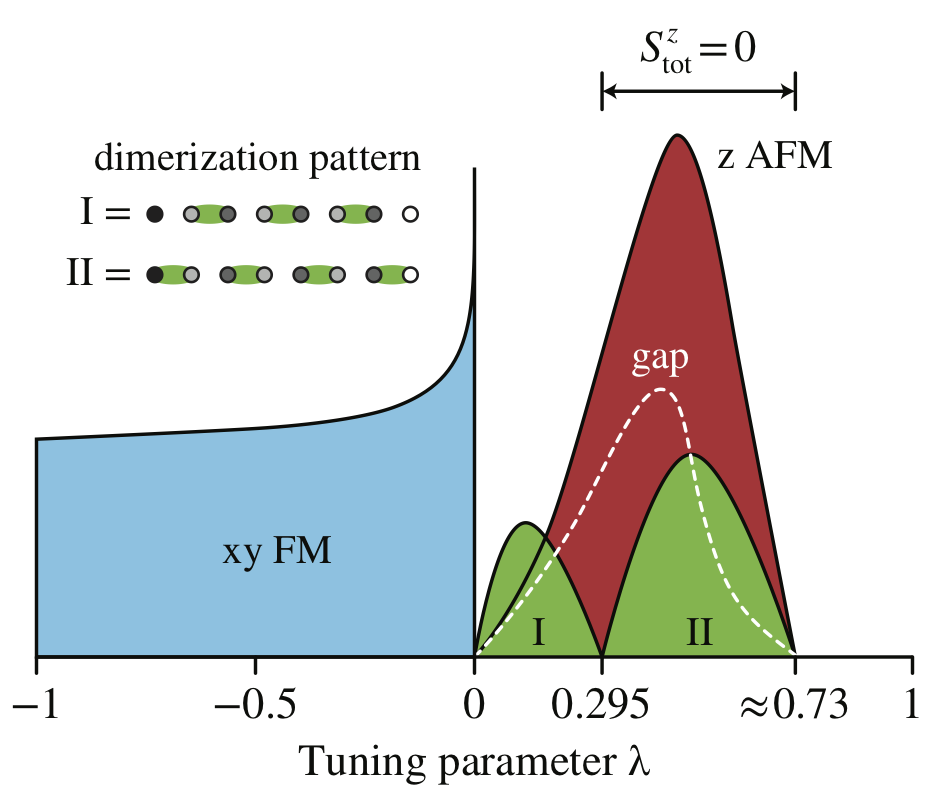
The Fredkin model describes a spin-half chain segment subject to three-body, correlated-exchange interactions and twisted boundary conditions. The model is frustration-free, and its ground state wave function is known exactly. Its low-energy physics is that of a strong xy ferromagnet with gapless excitations and an unusually large dynamical exponent. We study a generalized spin chain model that includes the Fredkin model as a special tuning point and otherwise interpolates between the conventional ferromagnetic and antiferromagnetic quantum Heisenberg models. We solve for the low-lying states, using exact diagonalization and density-matrix renormalization group calculations, in order to track the properties of the system as it is tuned away from the Fredkin point; we also present exact analytical results that hold right at the Fredkin point. We identify a zero-temperature phase diagram with multiple transitions and unexpected ordered phases. The Fredkin ground state turns out to be particularly brittle, unstable to even infinitesimal antiferromagnetic frustration. We remark on the existence of an “anti-Fredkin” point at which all the contributing spin configurations have a spin structure exactly opposite to those in the Fredkin ground state.
@article{
title = {Deforming the Fredkin spin chain away from its frustration-free point},
author = {Adhikari, Khagendra and Beach, K. S. D.},
journal = {Physical Review B},
volume = {99},
issue = {5},
pages = {054436},
numpages = {10},
year = {2019},
month = {Feb},
publisher = {American Physical Society},
doi = {10.1103/PhysRevB.99.054436},
url = {https://journals.aps.org/prb/abstract/10.1103/PhysRevB.99.054436}
}