Detection of symmetry-protected topological order in AKLT states by exact evaluation of the strange correlator
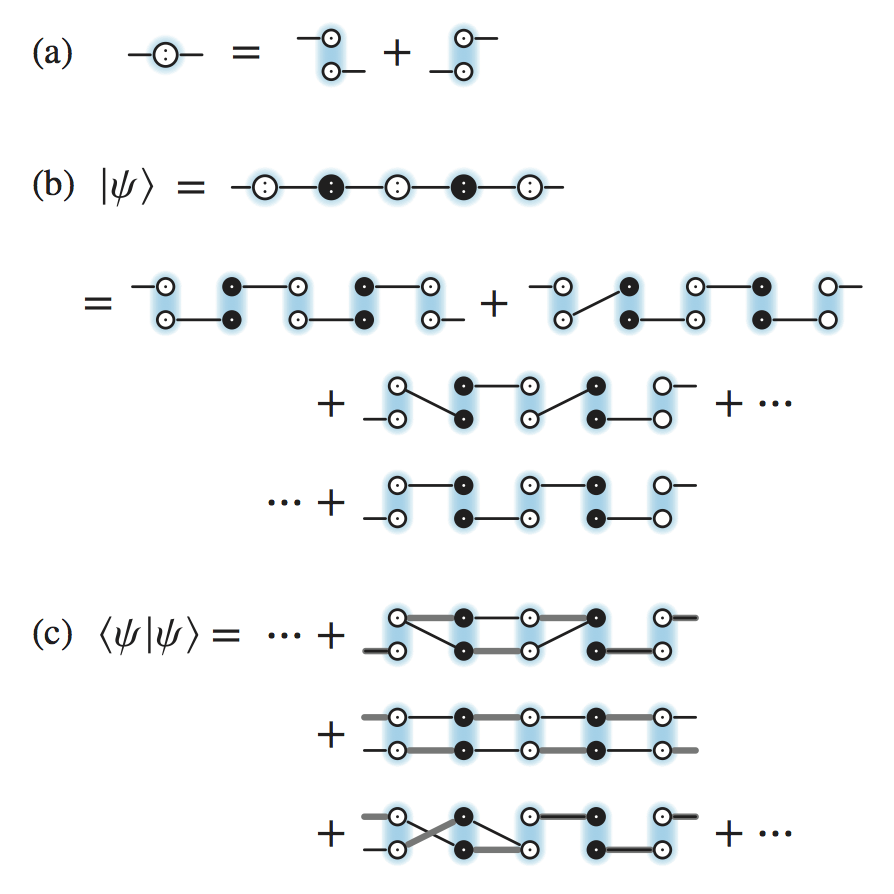
The strange correlator [Phys. Rev. Lett. 112, 247202 (2014)] has been proposed as a measure of symmetry protected topological order in one- and two-dimensional systems. It takes the form of a spin-spin correlation function, computed as a mixed overlap between the state of interest and a trivial local product state. We demonstrate that it can be computed exactly (asymptotically, in the Monte Carlo sense) for various Affleck-Kennedy-Lieb-Tasaki states by direct evaluation of the wave function within the valence bond loop gas framework. We present results for lattices with chain, square, honeycomb, cube, diamond, and hyperhoneycomb geometries. In each case, the spin quantum number S is varied such that 2S (the number of valence bonds emerging from each site) achieves various integer multiples of the lattice coordination number. We introduce the concept of strange correlator loop winding number and point to its utility in testing for the presence of symmetry protected topological order.
@article{Wierschem-PRB-16,
title = {Detection of symmetry-protected topological order in AKLT states by exact evaluation of the strange correlator},
author = {Wierschem, Keola and Beach, K. S. D.},
journal = {Phys. Rev. B},
volume = {93},
issue = {24},
pages = {245141},
numpages = {16},
year = {2016},
month = {June},
publisher = {American Physical Society},
doi = {10.1103/PhysRevB.93.245141},
url = {http://link.aps.org/doi/10.1103/PhysRevB.93.245141}
}