Dynamic Buckling and Fragmentation of Brittle Rods
J.R. Gladden, University of MississippiAndrew Belmonte, The Pennsylvania State University
At the W. G. Pritchard Laboratories in the Math Department at Penn State we devised a simple experiment to investigate how a slender beam responds to an impulsive load along it's axis. High speed video uncovered some very interesting dynamics which we reported in Physical Review Letters (PRL 94, 035503 (2005)). Figure 1 shows frames of a video of a piece of pasta just after being struck by a projectile moving at 3.5 m/s. A well defined buckling wavelength emerges.
A video of breaking pasta can be viewed here: Hit with a 4 m/s projectile or a 40 m/s projectile.

We applied linear stability analysis to a model of the stress wave propagating down the rod based on the results of Saint-Venant and the fourth order dynamical buckling PDE. This produced a prefered buckling wavelength [lambda] (the one that grows fastest) and growth rate [tau_b] of that mode. The expressions for these are listed below:
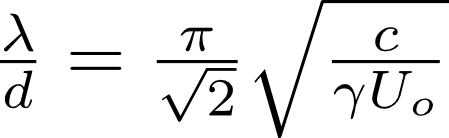
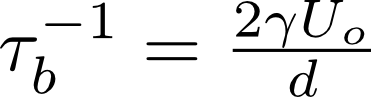
where c is the speed of sound in the material, d is the diameter of the circular cross-section, lambda is the wavelength and U_0 is the impact speed of the projectile.
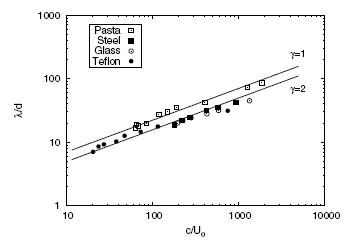
When we plot these scaling laws along with wavelength data obtained from the high speed video (shown below) we see excellent agreement. The only adjustment which needed to be made is to add a factor (gamma) which is either 1 if buckling sets in before the stress pulse reflects off the back end of the rod or 2 if the reflection occurs before buckling.
Fragmentation Statistics
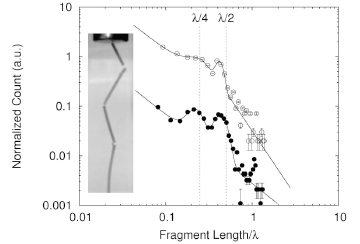
In a brittle rod, bending leads quickly to breaking. By shattering over 1000 pieces of pasta and measuring the length of each resulting fragment, we get the distribution shown below. It exhibits typical power law behavior except for two peaks. The center of these peaks corresponds to fragment lengths of 1/4 and 1/2 the buckling wavelength. 1/2 wavelength would be the distance between two successive curvature extrema and 1/4 wavelegth is the distance from the end of the rod and the first curvature extrema (see the still frame inset).