Chapter 23: Electric Fields

• Coulomb's law: F = k q₁q₂/r ² = 1/(4πε₀) q/r ², k = 8.99 · 10⁹ N·m²/C², ε₀ = 8.85 × 10^–12 C²/N·m².
• Fundamental charge: Value of the charge of an electron or proton, e = 1.60 × 10^–19 C .
• Electric field: E = F/q ; For a point charge, E = k q/r ² = 1/(4πε₀) q/r ².
• Electric field due to a charge distribution: Sum individual contributions or integrate, E = k ∫ (dq/r³) r .

Chapter 24: Gauss' Law

• Electric flux: For constant E, flat surface, Φ_E = (E cosθ) A = E · A. In general, Φ_E = ∫ E · dA .
• Gauss' law: The electric flux through a closed Gaussian surface is Φ_E = q_in/ε₀.
• At the surface of a conductor: It has to be perpendicular to the surface, and its magnitude is E = σ/ε₀.
• Large plate: Non-conducting E = σ/2ε₀ on both sides; Between plates with opposite charges, E = σ/ε₀.

Chapter 25: Electric Potential

• Electric potential energy: As for any conservative force, U = –W_PO.
• Electric potential: Defined as V = U/q = –W_PO/q ; In terms of E, V(P) = –∫ E · ds and E_s = –∂V/∂s .
• Examples: For a point charge V = k q/r ; Potential energy of a 2-point-charge system U = k q₁q₂/r ; For a charge distribution add the single-charge contributions, or set up an integral, V = k ∫ dq/r .

Chapter 26: Capacitance and Dielectrics

• Capacitance: Defined by C = Q/V ; For a parallel-plate capacitor, C = ε₀A/d.
• Capacitor combinations: In series, C_eq^–1 = C₁^–1 + C₂^–1 + ...; In parallel, C_eq = C₁ + C₂ + ...
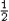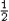• Electric energy: In a capacitor, U = QV ; Energy density in an electric field u = U/volume = ε₀E².
• Dielectrics: The permittivity of the vacuum gets replaced by ε = ε₀κ; For example, C = ε A/d = κε₀ A/d.

Chapter 27: Current and Resistance

• Electric current: I = dQ/dt , or Q = ∫ I(t) dt ; Current density defined by I = ∫ J · dA; Also, J = nev_d.
• Ohm's law: Relationship between potential difference and current, I = V/R ; also E = ρJ, or J = σE.
• Resistance: For a uniform block of length L and cross-sectional area A, R = ρL/A .
• Power: In general, P = IV. For current through a resistor, P = I²R = V²/R.

Chapter 28: Direct-Current Circuits

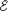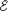• Emf: The amount of amount of work done per unit charge = dW/dq; With internal resistance V = – Ir.
• Resistor combinations: In series R_eq = R₁ + R₂ + ...; In parallel R_eq^–1 = R₁^–1 + R₂^–1 + ...
• RC circuits: τ = RC; Charge V(t) = V₀ (1 – e^–t/RC) and q(t) = Q (1 – e^–t/RC); DischargeV(t) = V₀ e^–t/RC .