Rays
and Shadows
- Rays: In what circumstances we can assume that light travels
along straight lines and casts sharp shadows beyond edges of extended
objects, and why. What is geometric optics?
- Shadows: What are umbra and penumbra, how does one draw them;
Be able to calculate their extent in specific situations; Their
relation to the phenomenon of eclipses.
Reflection
and Mirrors
- Reflection: Diffuse vs specular reflection; Use of the law
of reflection,
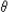 i = i = 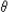 r,
M = 1. r,
M = 1.
- Flat mirrors: Properties of the image; Use of geometry in
problems with flat mirrors.
- Curved mirrors: Convex vs concave mirrors; parabolic vs spherical
mirrors.
- Important concepts: Center, principal axis, vertex, focal
point, focal length f = R/2 (including sign); Concept
of aberrations in general and spherical aberration; Real vs virtual
images.
- Mirror equation: The object and image positions are related
by 1/so + 1/si =
1/f; each of the three quantities is positive if it refers
to a location in front of the mirror, negative if behind.
- Magnification: By definition, m = hi/ho;
Its value is equal to m = –si/so.
- Problem solving: Be able to apply both graphical method (ray
tracing) and analytical method (mirror and magnification equations).
Refraction
- Refraction: Understand the general idea; The index of refraction
of a transparent substance is n = c/v, where v is
the speed of light in that material; it often depends on the wavelength.
- Snell's law: For light entering medium 2 from medium 1, n1 sin
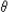 1 = n2 sin 1 = n2 sin
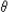 2. 2.
- Total internal reflection: Occurs when n2 <
n1 and the angle of incidence
is larger than the critical angle
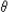 c satisfying
sin c satisfying
sin 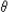 c =
n2/n1. c =
n2/n1.
|