Waves: Main Concepts

• Types: What is a wave? Different materials (string, air, water surface, ...., non-mechanical waves), shapes (pulse, continuous, periodic, harmonic wave), directions of oscillation (transverse vs longitudinal); Be able to come up with an example for each type.
• First concepts: Amplitude, period, frequency (f = 1/T), wavelength.
• Speed: Speed of wave as opposed to speed of point in the medium. Relation to wavelength and frequency, v = 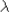f; In the case of a wave on a string of mass per unit length m/L, under a tension F_T, v = [F_T/(m/L)]^1/2.
• Intensity: Energy per unit time per unit surface, I = (power)/(surface area).

Waves: Effects

• Propagation in different media: Conceps of reflection and transmission; Difference between effect of open ends and fixed ends in the case of a string; Concepts of wave front and ray.
• Interference: Superposition and interference; Types, constructive and destructive.
• Standing waves: When can one get them? Resonant frequency, fundamental and higher harmonics, nodes and antinodes. When both ends are nodes or antinodes, L = n (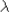_n/2); when one is an antinode and the other a node, L = n (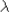_n/4) with n odd.

Sound: First Concepts

• General concept: What is sound (what type of wave)? Difference between viewing it as a displacement wave or a pressure wave.
• Speed: Value in air at standard temperature and pressure, v_sound = 340 m/s.
• Frequency and pitch: [Relationship between those two concepts]; Audible range of frequencies, from about 20 Hz to about 20,000 Hz; Infrasound and ultrasound.
• Beats: When do they occur? The frequency of the beats is the difference between the two frequencies involved, f_beat = f₁ – f₂.

Intensity and Loudness

• Intensity: Range from I₀ = 10^–12 W/m² (below is inaudible) to 1 W/m² (threshold of pain).
• Loudness: Relationship between loudness and intensity.
• Sound level: Defined as 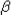= 10 Log (I / I₀), expressed in dB.
• Applications: Audible range in terms of decibels; Be able to relate changes in intensity to changes in sound level using properties of logarithms.