Main
Kinematical Quantities
- Introductory concepts: Axis of rotation; Expressing angles
in radians.
- Angular displacement:
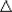 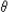 = = 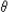 2 – 2 – 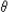 1,
usually measured in radians in this chapter. 1,
usually measured in radians in this chapter.
- Frequency: The rate at which the number of turns changes
in time, f =
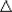 n / n / 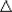 t. t.
- Angular velocity: The rate at which
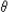 changes
in time, changes
in time, 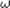 =
limit of =
limit of 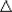 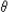 / / 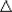 t for
small t for
small 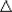 t. t.
- Angular acceleration. The rate at which
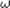 changes, changes, 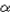 =
limit
of =
limit
of 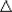 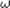 / / 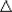 t for
small t for
small 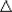 t. t.
- Relationship with linear motion: d = r
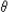 ,
v = r ,
v = r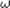 ,
at = r ,
at = r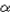 ,
aR = ,
aR = 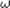 2r or
v2/r. 2r or
v2/r.
Rotational Dynamics
- Torque: The torque of a force F applied a distance r from
an axis is
 =
rF sin =
rF sin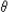 . .
- Moment of inertia: For an extended object, use a table; For
a composite object, add all the individual moments of inertia; For
a particle,
I = mr2 .
- Newton's 2nd law for rotations: Relation torque-angular acceleration,
 net =
I net =
I 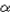 . .
- Rotational kinetic energy: KErot =
I
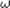 2 /
2. This kinetic energy is used when rotation is involved, in the same
equations as the translational kinetic energy, for example the conservation
of energy equation. 2 /
2. This kinetic energy is used when rotation is involved, in the same
equations as the translational kinetic energy, for example the conservation
of energy equation.
- Angular momentum: L = I
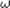 ;
When is the angular momentum of a system conserved? ;
When is the angular momentum of a system conserved?
Examples and Problems
- Rolling motion: Be able to apply the no-slipping
condition
v = r
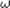 to
a problem. to
a problem.
- Problem solving: Be able to apply Newton's second law (for
translation and for rotation), or conservation of energy, or conservation
of angular momentum, as appropriate to each problem.
|