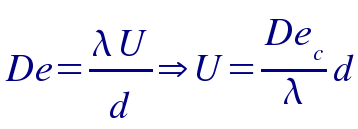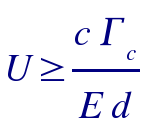How
the fluid responds
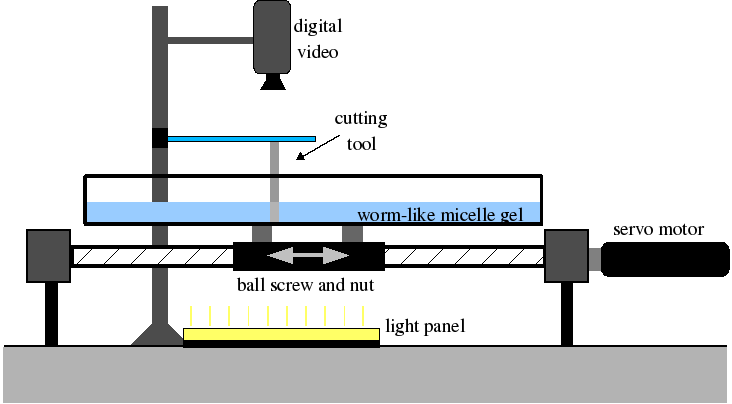
By varying the speed (U) and diameter (d) of the rod moving through the
fluid, we observed three distinct responses which are shown in the left
image above.
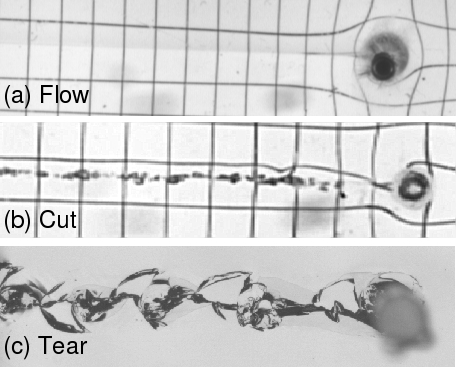
Flow was
very smooth fluid movement of the fluid around the approaching cylinder
and recombining behind it with no air gaps, but leaving a shallow
crease in the surface which lasts on the order of a minute. The
Cut phase occurs when the cylinder
speeds up so that a small air gap forms behind the cylinder and the
wake walls become textured. As the wake walls recombine, air
bubbles are trapped leaving a trail. The
Tear phase occurs when the speed of
the cylinder further increases so that extensional stresses in the wake
walls become so great the the wall splits generating a crack
propagating laterally into the fluid. These three phases of the
fluid response are fully mapped out in the phase diagram shown in the
right panel of the figure above. The solid curves indicate phase
boundaries.
The linear Cut - Flow boundary can be readily explained using an stress
relaxation argument, or in the language of fluid dynamics, a critical
Deborah (De) number. De is a ratio of the relaxation
time to the flow time scale and for a fluid moving around
a cylinder it is
We see the linear scaling and our fitted slope and measured relaxation
time of 1.1 seconds from rheology experiments gives us a critical
Deborah number of 1. This means the onset of the cutting phase
occurs when the fluid tries to flow faster than the relaxation time
allows. It therfore must relieve the energy by small tears on the
surface producing the texturing in the walls.
The Tearing boundary scaling of U ~ 1/d is much more difficult to
derive. This is mainly because it involves the initiation and
propagation of a crack into a highly viscoelastic material and the
theory for this is poorly understood. However, using a simple
critical line stress argument and an estimate for the force exerted on
the wake walls by the cylinder, we can derive a scaling law which does
seem to agree with our observations:
where c is the speed of sound, E is Young's modulus, and /Gamma_c is
the critical line force or tearing strength for the material.
What else did we see?
We observed a wide variety of interesting dynamics such as a crack that
occurs in front of the cylinder which oscillates about the line of
motion, very characterstic shark fin like tearing patterns as shown
above, and unique birefringent stress patterns which depend on the
geometry of the cutting tool.