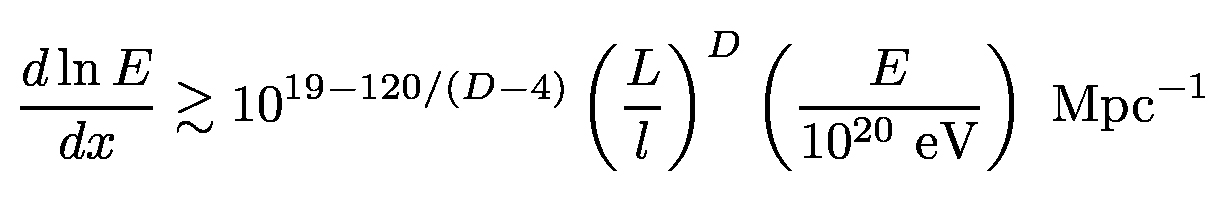Gravitational diffraction radiation
Vitor Cardoso
Department of Physics and Astronomy, The University of Mississippi, University, MS 38677-1848, USA
Marco Cavaglià
Department of Physics and Astronomy, The University of Mississippi, University, MS 38677-1848, USA
Mário Pimenta
Departamento de Física, IST, Av. Rovisco Pais, 1049-001 Lisboa, Portugal
and
LIP, Av. Elias Garcia, 14-1, 1000-149 Lisboa, Portugal
(Dated: November 7, 2006)
We show that if the visible universe is a membrane embedded in a higher-dimensional space, particles in
uniform motion radiate gravitational waves because of spacetime lumpiness. This phenomenon is analogous
to the electromagnetic diffraction radiation of a charge moving near to a metallic grating. In the
gravitational case, the role of the metallic grating is played by the inhomogeneities of the
extra-dimensional space, such as a hidden brane. We derive a general formula for gravitational
diffraction radiation and apply it to a higher-dimensional scenario with flat compact extra dimensions.
Gravitational diffraction radiation may carry away a significant portion of the particle's initial
energy. This allows to set stringent limits on the scale of brane perturbations. Physical effects of
gravitational diffraction radiation are briefly discussed.
I. INTRODUCTION
Larmor's formula of
electromagnetism [1] states that an electric charge in uniform motion does not
radiate. However, there are two ways to have radiation from a charge moving with constant velocity. The first
way is to have a particle moving in a medium with velocity exceeding the phase velocity of light in that
medium. This gives rise to the well-known Vavilov-Cherenkov radiation [1-3]. The
second way is to consider charge motion in inhomogeneous media. Ginzburg and Frank [2] first discussed this effect by investigating a particle in uniform motion which
crosses a planar interface between two media with dissimilar refractive index. This kind of radiation is
known as transition
radiation [1]. More generally, any motion near finite-size objects
also induces radiation, in a process called diffraction radiation [4]. One of the
first experimental verifications on this effect was provided by Smith and Purcell [5]. The Smith-Purcell experimental set-up consisted of an electron moving close to
the surface of a metal diffraction grating at right angles to the rulings. The theory of the Smith-Purcell
effect has been discussed by several authors [6]. The aim of this paper is to
show the existence of gravitational diffraction radiation (GDR) and discuss its physical effects. The model
under consideration is a braneworld scenario [7] such as, for example, the Randall-Sundrum I model
[8]. Braneworld models have attracted a lot of interest in recent years,
revolutionizing our view of how our universe may be described. The central idea of braneworld scenarios is
that the visible universe is restricted to a four-dimensional brane inside a higher-dimensional space, called the bulk. The additional
dimensions are taken to be compact and other branes may be moving through the bulk. Interactions of the
visible brane with the bulk and hidden branes introduce effects not seen in standard physics.
In this set-up, a particle in uniform motion on the visible brane radiates gravitational waves due to the
presence of a second (hidden) brane at finite distance, which plays the role of the metal diffraction grating
of the Smith-Purcell experiment. GDR on the visible brane is generated by inhomogeneities on the hidden brane
due, for example, to bulk-brane interactions and brane fluctuations [9]. We will
show that the amount of GDR depends on the size of extra dimensions and the length scale of brane
perturbations. This result is general and independent on the fine details of the model. Without loss of
generality, in our computations we will consider a flat five-dimensional spacetime with the extra dimension
taking values within the interval [0,L]. The distance between the particle and the diffraction
grating, h = L/2, is the distance between the two branes located at the orbifold fixed points. The
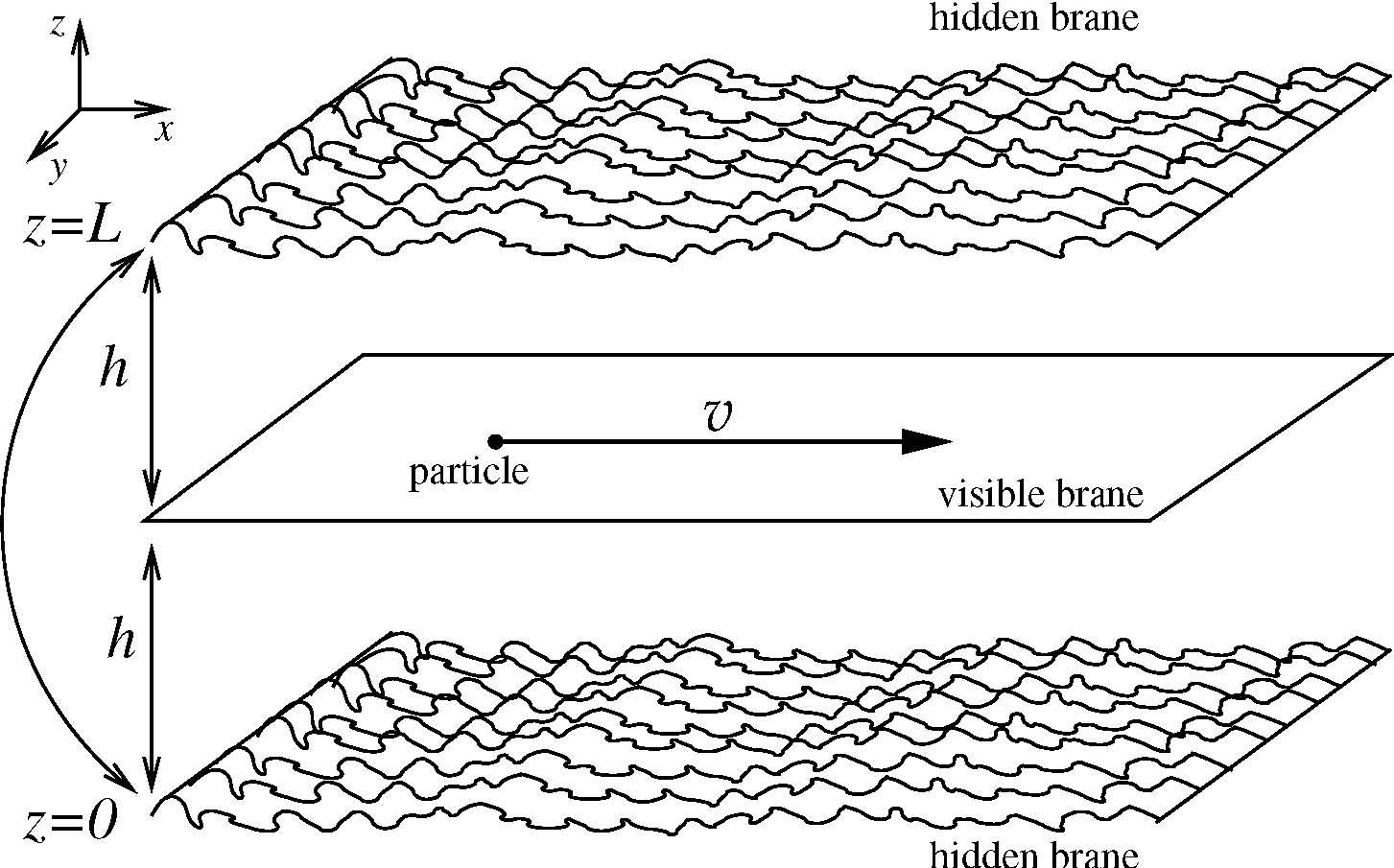
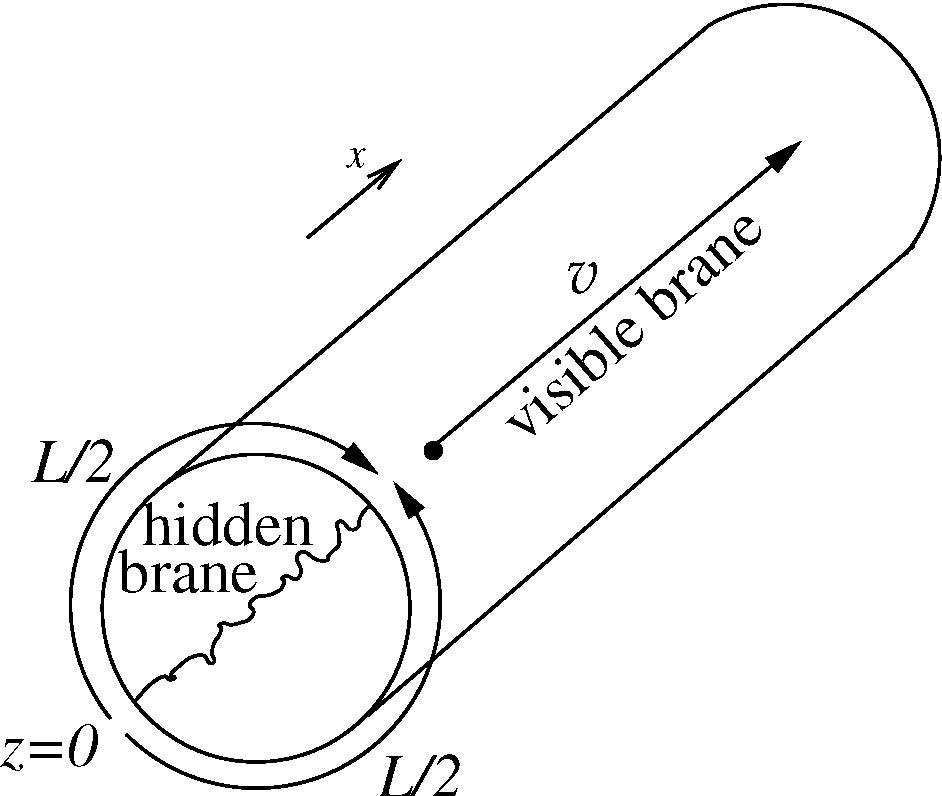
model is illustrated pictorially in Fig. 1. The generalization to higher-dimensions is trivial and is
discussed at the end of this letter.
 |
 |
|
FIG. 1: Pictorial representation of the braneworld scenario considered in the text. The hidden brane at
z=0 is identified with the brane at z=L. The visible brane is located at z=h=L/2. The
particle moves on the visible brane along x with constant velocity v. Only one transverse
coordinate, y, is shown. The right panel shows the wrapping around the extra dimension z. If
the two halves of the cylinder are identified, the Randall-Sundrum model I [8] is obtained.
|
II. THEORY OF GRAVITATIONAL DIFFRACTION RADIATION
In the harmonic
gauge, the five-dimensional linearized Einstein equations are
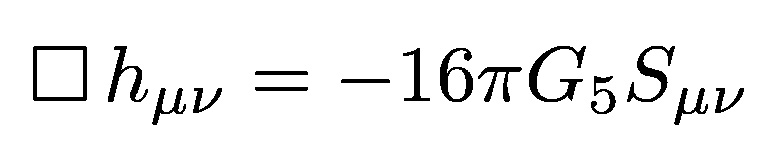 |
(1) |
where hμν represents small corrections to the flat background and
Sμν is the modified energy-momentum tensor of the source [10]. For sake of computational simplicity, we
replace the the gravitational field components with a single scalar degree of freedom, i.e. rewrite the above equation
as 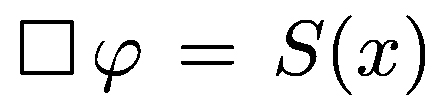 . This is a common procedure [11].
If we carefully select S(x), the scalar field φ can mimic all aspects of gravitational
waves (except polarization) [12]. The source of the field is a minimally coupled
pointlike particle with nonzero mass m. If we represent its worldline by
xμ=xμ(τ), where τ is the proper time, φ
satisfies the inhomogeneous wave equation
. This is a common procedure [11].
If we carefully select S(x), the scalar field φ can mimic all aspects of gravitational
waves (except polarization) [12]. The source of the field is a minimally coupled
pointlike particle with nonzero mass m. If we represent its worldline by
xμ=xμ(τ), where τ is the proper time, φ
satisfies the inhomogeneous wave equation
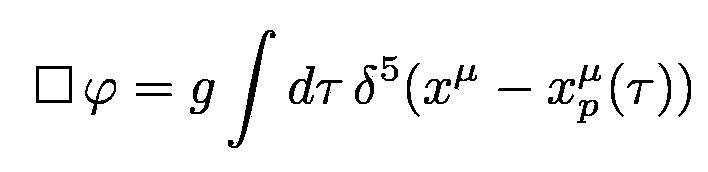 |
(2) |
where g is the coupling
constant. We consider a particle in uniform motion on the visible brane. Denoting with z
the coordinate transverse to the brane and with y1, y2 the longitudinal
coordinates perpendicular to the particle direction of motion x, the particle worldline in the brane
reference frame is xμ(τ)= (t =γτ, x = vt, y1 = 0, y2 =
0, z = h), where γ is the Lorentz factor of the particle. The time-averaged energy radiated per unit time in
the direction n is
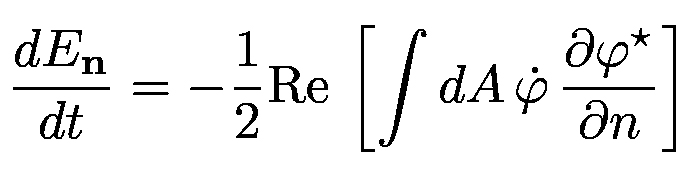 |
(3) |
where dA is the surface element with normal n. If the tensor structure of the gravitational perturbations is
taken into consideration, the source term in Eq. (2) must be changed into
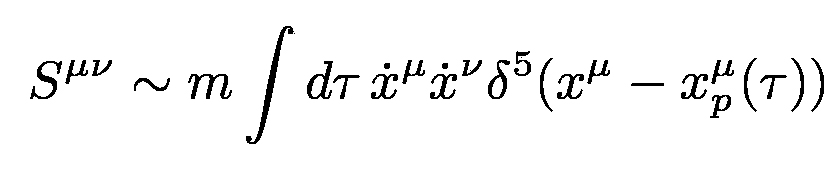 |
(4) |
The results for the scalar field can be translated to the gravitational case by setting 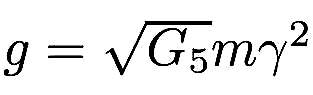 [12].
[12].
If the branes are smooth, a particle with constant velocity does not radiate. This can be checked by deriving
the Larmor's formula
for the field. In order to avoid complications due to the higher-dimensional nature of the spacetime [10, 11, 13], we temporarily assume that there is only one transverse spatial
dimension. The total power emitted per unit of solid angle in the direction n is
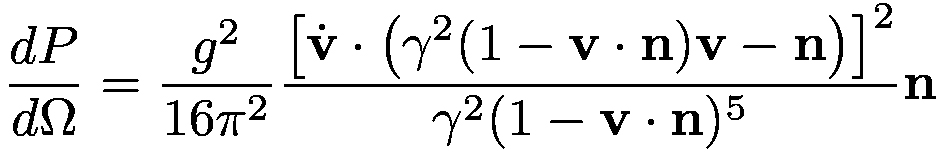 |
(5) |
Thus a particle in uniform motion in empty space (on the brane) does not radiate. If a hidden brane is
present, the Green's
function has to be modified to take into account its effects. The hidden brane can be thought as a
wall parallel to the particle direction of propagation at distance h. By repeating the steps leading
to Eq. (5) it is straightforward to show that there is no radiation for uniform motion parallel to the wall.
This result can be understood by boosting the solution to the rest frame of the particle. The problem is
reduced to a static problem with one image particle on the other side of the wall. Clearly, the reduction to the static
configuration is only possible if the brane is smooth and infinite in the x direction. If the brane is
inhomogeneous in the particle direction of propagation, diffraction radiation is generated. In that case, the
image configuration is time dependent and the system is equivalent to a set of oscillating charges in the
particle reference frame. Diffraction radiation can be understood as being generated by the reflection of the
boosted static field on the nearby wall.
 |
|
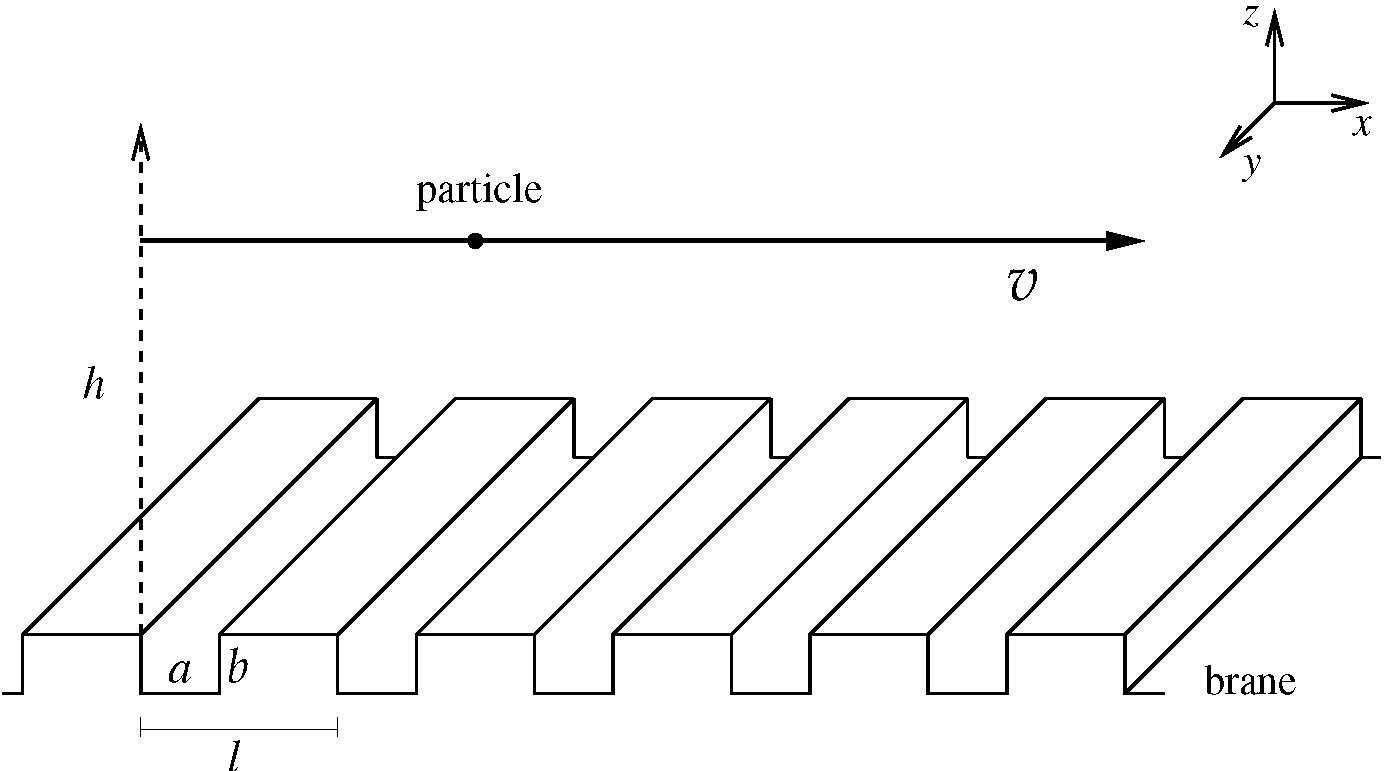
FIG. 2: Pictorial representation of brane perturbations. The longitudinal brane perturbations are periodic
in x with length l. The transverse perturbations have length b. Only one transverse
coordinate, y, is shown.
|
We now compute the radiated power in the presence of a brane with typical longitudinal perturbations of
length scale l and transverse perturbations of length scale b. These perturbations are modeled with a
l-periodic lamellar grating with rulings of width a perpendicular to the particle direction of motion
as in Fig. 2. (The Smith-Purcell effect for a single grating with these characteristics has been discussed in
Ref. [14].) Although this model is clearly an oversimplification, its main
features do not depend on the choice of the perturbation structure: The existence of diffraction radiation is
due to the excitation of propagating modes by evanescent waves and is independent of the particular
mechanism by which the propagating modes are excited. The calculation with a perturbed brane can be
conveniently solved by considering the Fourier transform of the field φ:
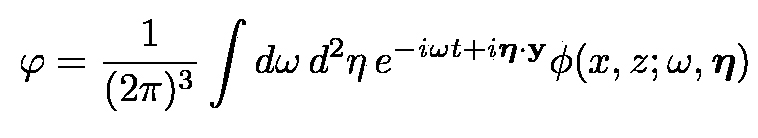 |
(6) |
The field equation in the Fourier space is
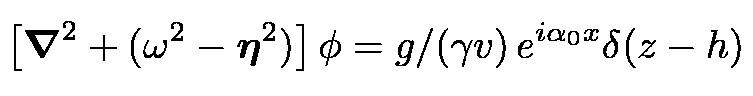 |
(7) |
where 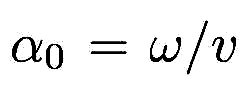 . The general solution for the field
. The general solution for the field 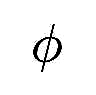 in the bulk is the sum of the inhomogeneous solution of the above equation plus a
superposition of plane wave solutions of the two-dimensional Helmholtz equation:
in the bulk is the sum of the inhomogeneous solution of the above equation plus a
superposition of plane wave solutions of the two-dimensional Helmholtz equation:
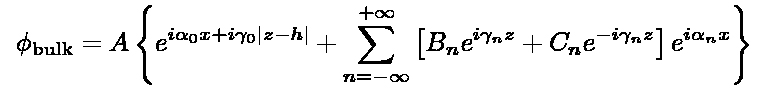 |
(8) |
where 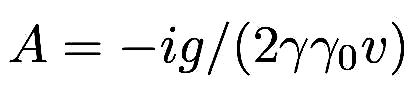 ,
, 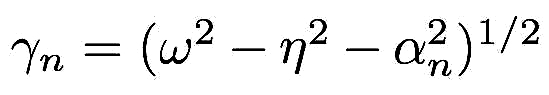 and
and 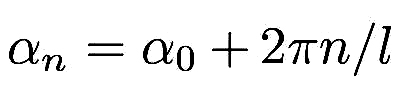 . Since the parameter
. Since the parameter 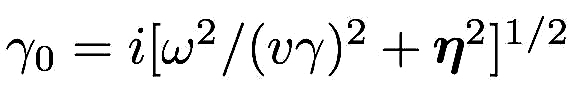 is
pure imaginary, the first term in Eq. (8) describes an evanescent wave that decays exponentially with increasing
distance from the particle trajectory. This evanescent wave is the non-propagating part of the spectrum due to the
particle in uniform motion. The second term in Eq. (8) represents a superposition of propagating plane waves.
The physical interpretation of these propagating modes is that of radiation arising from the modes of the
brane perturbations, which are excited by the evanescent waves. The amplitude
is
pure imaginary, the first term in Eq. (8) describes an evanescent wave that decays exponentially with increasing
distance from the particle trajectory. This evanescent wave is the non-propagating part of the spectrum due to the
particle in uniform motion. The second term in Eq. (8) represents a superposition of propagating plane waves.
The physical interpretation of these propagating modes is that of radiation arising from the modes of the
brane perturbations, which are excited by the evanescent waves. The amplitude 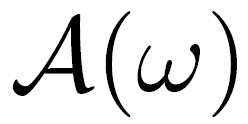 of the GDR is thus expected to be of the order of the amplitude of the non-propagating modes,
i.e.,
of the GDR is thus expected to be of the order of the amplitude of the non-propagating modes,
i.e.,
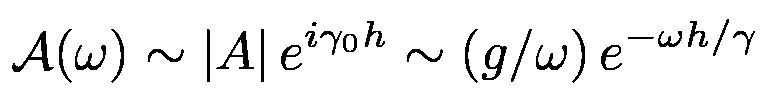 |
(9) |
where we have taken the relativistic limit γ>>1. This can be shown by computing the
amplitudes of the radiating modes as function of the evanescent wave amplitude A. The solution in
the bulk must match the solution on the brane
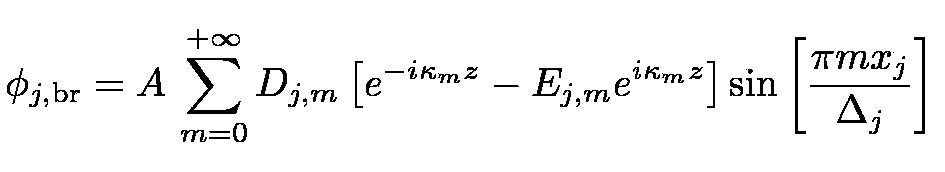 |
(10) |
where 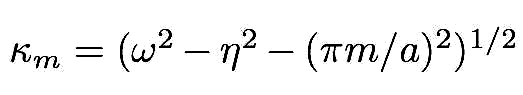 and
and 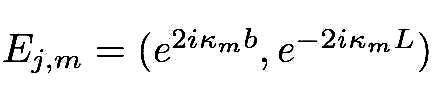 ,
xj = (x, x-a) and Δj = (a, l-a) in the intervals x∈[0, a]
(j = 1) and x∈[a, l] (j = 2), respectively. Choosing Dirichlet boundary conditions, the amplitudes of the propagating waves
satisfy the system of linear inhomogeneous algebraic equations:
,
xj = (x, x-a) and Δj = (a, l-a) in the intervals x∈[0, a]
(j = 1) and x∈[a, l] (j = 2), respectively. Choosing Dirichlet boundary conditions, the amplitudes of the propagating waves
satisfy the system of linear inhomogeneous algebraic equations:
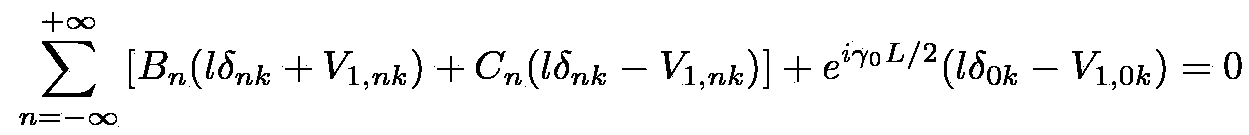 |
(11) |
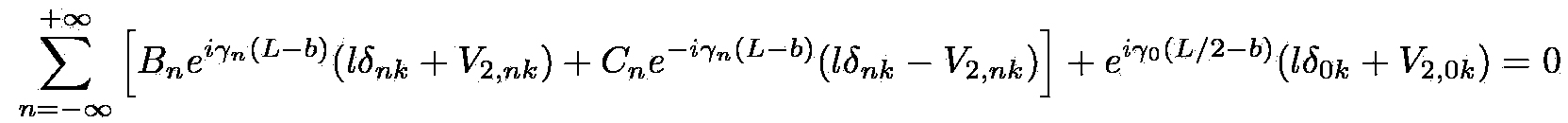 |
(12) |
where
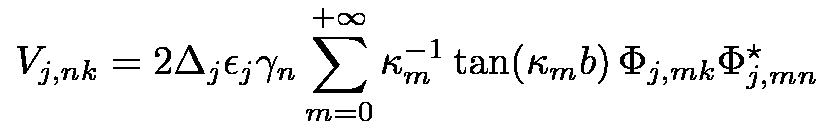 |
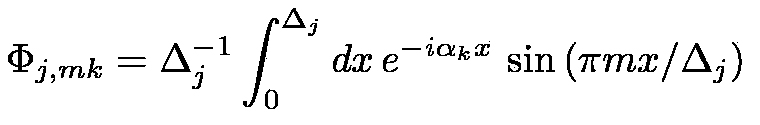 |
(13) |
and 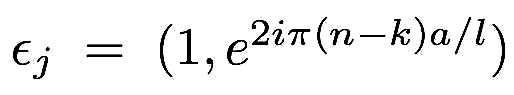 . The power emitted in the bulk follows from Eq.
(3) after solving Eqs. (12) for the propagating wave amplitudes Bn and
Cn. Generalizing to D spacetime dimensions and taking the relativistic limit, we
have
. The power emitted in the bulk follows from Eq.
(3) after solving Eqs. (12) for the propagating wave amplitudes Bn and
Cn. Generalizing to D spacetime dimensions and taking the relativistic limit, we
have
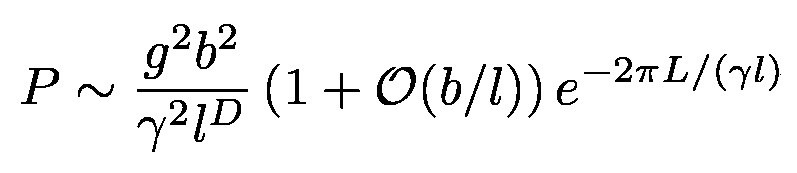 |
(14) |
where we have set l = 2a and assumed small b/l. Since we assumed the source to be
pointlike, Eq. (14) is valid for particle size L, b and l, otherwise it describes
the diffraction radiation of a relativistic particle under very general assumptions. The GDR energy loss
per unit distance is
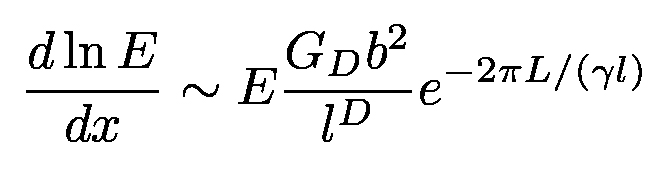 |
(15) |
where GD is the D-dimensional Newton constant.
BOUNDS ON BRANE INHOMOGENEITIES
As an example of the physical consequences of GDR, let us consider the scenario with D-4 large extra
dimensions of size L [15]. In this model GD is related to the
four-dimensional Newton
constant G4 by GD∼LD-4G4. There are
two natural length scales, the Planck length, LPl∼10-17 cm, and the size of the
large extra dimensions, L ∼1030/(D-4)-17 cm. The perturbation length scales l
and b are expected to be larger than the Planck length. This implies 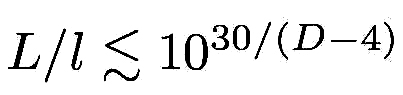 and
and 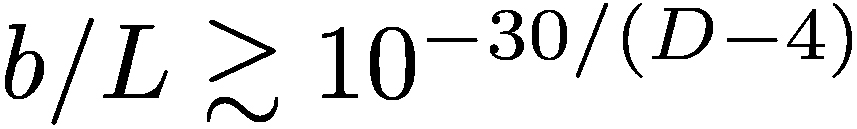 . The largest γ factors are
observed in ultra high-energy cosmic rays, reaching 1011 [16]. In this case, the exponential in Eq. (15) can be set to unity for all
D>6. Using the above constraints, we obtain
. The largest γ factors are
observed in ultra high-energy cosmic rays, reaching 1011 [16]. In this case, the exponential in Eq. (15) can be set to unity for all
D>6. Using the above constraints, we obtain
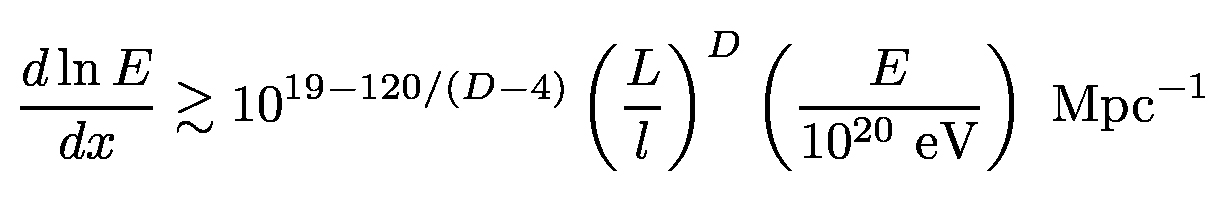 |
(16) |
Equation (16) imposes stringent limits on the smoothness of the brane. Upper bounds on L/l range from
103 for D=7 to ≤ 1 for D≥ 9. Therefore, GDR implies that the brane must
be smooth on scales of order of the size of the large extra dimensions, i.e., on scales much larger than the
Planck length. This
fact has important consequences for the problem of initial conditions in models of brane cosmology. (See,
e.g, Ref. [17].)
IV. DISCUSSION
In higher-dimensional models of our universe, particles radiate gravitational waves due to the structure of
the extra dimensions, specifically the presence of an inhomogeneous hidden brane. We have called
this phenomenon "Gravitational Diffraction Radiation" because of its similarity with the electromagnetic
diffraction radiation which is emitted by a charge moving near a metallic grating. GDR is a general
phenomenon of all higher-dimensional braneworld scenarios. It applies to particles propagating both on the brane and in
the bulk. As an example of its physical effects, we have discussed the GDR emitted by a particle on the
visible brane and derived lower bounds on the scale of brane perturbations.
The above results can be extended in several directions. For instance, this paper considers only
inhomogeneities on the hidden brane. The visible brane is also inhomogeneous. Therefore, free motion on the visible brane is not uniform
from the five-dimensional perspective. This effect could be comparable to the GDR effect studied here. The
derivation of GDR presented above is purely classical. Although the scale of brane
inhomogeneities suggests that the system can be treated as classical, the importance of quantum effects
should be assessed. It would also be interesting to consider GDR emitted by photons or bulk particles. In
the latter case, GDR energy loss would manifest itself as a background of stochastic gravitational waves on
the visible brane.
GDR is originated by the lumpiness of the spacetime at small scales. Thus GDR effects may show up in a
variety of physical situations besides braneworld models. Emission of radiation by free particles in a cosmic
string background was discussed in Ref. [18]. GDR could also play an important
role in the very early universe or near the horizon of black holes. Direct signatures are unlikely to be
observed in these cases. However, GDR emission could lead to interesting predictions at theoretical level
and possibly indirect observable effects.
Acknowledgements
We thank Alikram Aliev, Luca Bombelli and Roy Maartens for discussions
and useful suggestions. VC acknowledges financial support from Fundaçao Calouste Gulbenkian through
the Programa Gulbenkian de Estìmulo à Investigaçao Cientìfica.
References
[1] J. D. Jackson, Classical Electrodynamics, (J. Wiley & Sons, NJ, 1999).
[2] V. L. Ginzburg and I. M. Frank, J. Phys. USSR, 9, 353 (1945); Zh. Eksp. Teor. Fiz. 16, 15 (1946).
[3] I. E. Tamm, General characteristics of radiations emitted by systems moving with super-light velocities with some applications
to plasma physics, Nobel lecture (1958).
[4] B. M. Bolotovskii and G.V. Voskresenski, Usp. Fiz. Nauk. 88, 209 (1966); Sov. Phys. -Usp. 9 73 (1966); B. M. Bolotovskii
and E. A. Galst'yan, Physics-Uspekhi 43(8), 755 (2000).
[5] S. J. Smith and E. M. Purcell, Phys. Rev. 92, 1069 (1953).
[6] See, e.g., G. Toraldo di Francia, Nuovo Cimento 16, 61 (1960); P. M. van den Berg, J. Opt. Soc. Am. 63, 1588 (1973);
ibid. 63, 1588 (1973).
[7] R. Maartens, Living
Rev. Rel. 7, 7 (2004).
[8] L. Randall and R. Sundrum, Phys. Rev. Lett. 83, 3370 (1999).
[9] M. Bando, T. Kugo, T. Noguchi and K. Yoshioka, Phys. Rev. Lett. 83, 3601 (1999).
[10] V. Cardoso, O. J. C. Dias and J. P. S. Lemos, Phys. Rev. D 67, 064026 (2003).
[11] A. O. Barvinsky and S. N. Solodukhin, Nucl. Phys. B 675, 159 (2003).
[12] C. W. Misner et al., Phys. Rev. Lett. 28 (1972) 998.
[13] H. Soodak and M.S. Tiersten Am. J. Phys. 61, 395 (1993); A. A. Ungar, Am. J. Phys. 62, 279 (1994).
[14] Y. Shibata et al., Phys. Rev. E 57, 1061 (1998); O. Haeberl´e, Electromagnetic radiation generated by relativistic electrons
interacting with a diffraction grating, PhD thesis, Université Louis Pasteur, 1994 (unpublished).
[15] N. Arkani-Hamed, S. Dimopoulos and G. R. Dvali, Phys. Lett. B 429,
263 (1998); I. Antoniadis, N. Arkani-Hamed, S. Dimopoulos and G. R. Dvali, Phys. Lett. B 436, 257 (1998).
[16] A. V. Olinto, Phys. Rept. 333, 329 (2000);
M. Nagano and A. A. Watson, Rev. Mod. Phys. 72, 689 (2000).
[17] J. Khoury, B. A. Ovrut, P. J. Steinhardt and N. Turok, Phys. Rev. D 64, 123522 (2001);
P. J. Steinhardt and N. Turok, Phys. Rev. D 65, 126003 (2002);
R. Kallosh, L. Kofman and A. D. Linde, Phys. Rev. D 64, 123523 (2001).
[18] A.N. Aliev and D. V. Gal'tsov, Annals of Physics 193, 142 (1989).


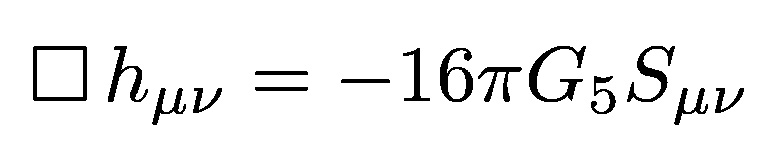
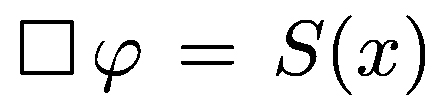 . This is a common procedure
. This is a common procedure 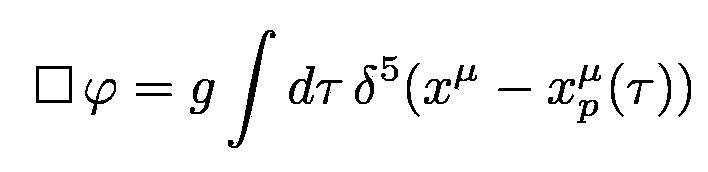
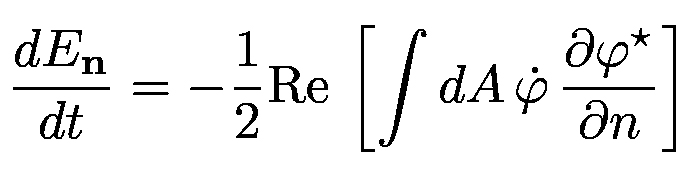
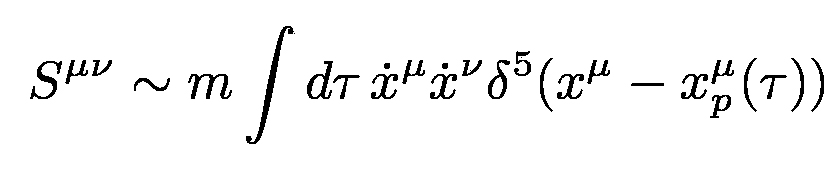
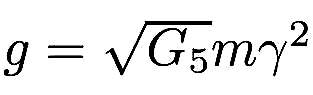
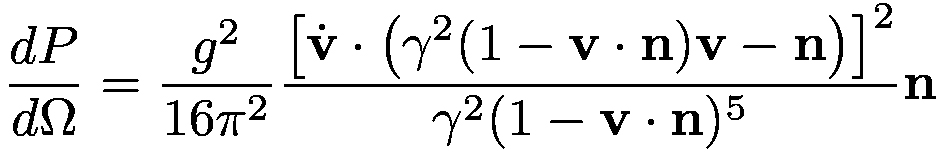

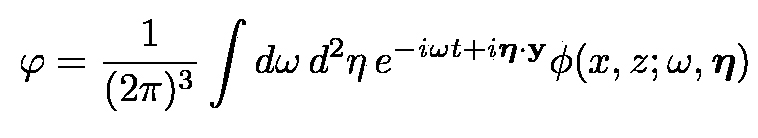
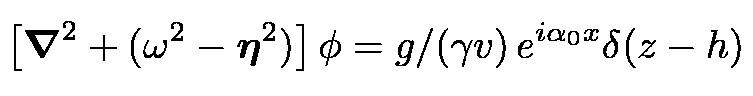
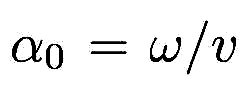 . The general solution for the field
. The general solution for the field 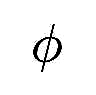 in the bulk is the sum of the inhomogeneous solution of the above equation plus a
superposition of plane wave solutions of the two-dimensional Helmholtz equation:
in the bulk is the sum of the inhomogeneous solution of the above equation plus a
superposition of plane wave solutions of the two-dimensional Helmholtz equation:
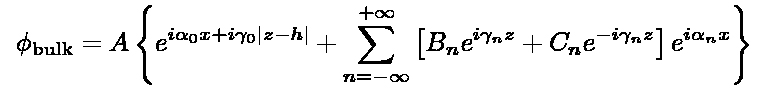
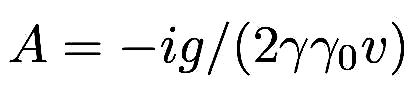 ,
, 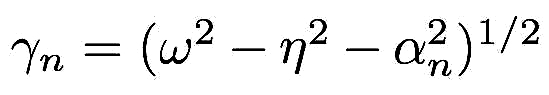 and
and 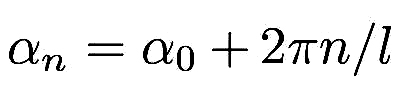 . Since the parameter
. Since the parameter 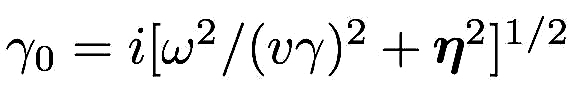 is
pure imaginary, the first term in Eq. (8) describes an evanescent wave that decays exponentially with increasing
distance from the particle trajectory. This evanescent wave is the non-propagating part of the spectrum due to the
particle in uniform motion. The second term in Eq. (8) represents a superposition of propagating plane waves.
The physical interpretation of these propagating modes is that of radiation arising from the modes of the
brane perturbations, which are excited by the evanescent waves. The amplitude
is
pure imaginary, the first term in Eq. (8) describes an evanescent wave that decays exponentially with increasing
distance from the particle trajectory. This evanescent wave is the non-propagating part of the spectrum due to the
particle in uniform motion. The second term in Eq. (8) represents a superposition of propagating plane waves.
The physical interpretation of these propagating modes is that of radiation arising from the modes of the
brane perturbations, which are excited by the evanescent waves. The amplitude 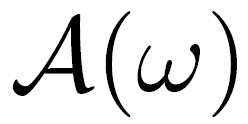 of the GDR is thus expected to be of the order of the amplitude of the non-propagating modes,
i.e.,
of the GDR is thus expected to be of the order of the amplitude of the non-propagating modes,
i.e.,
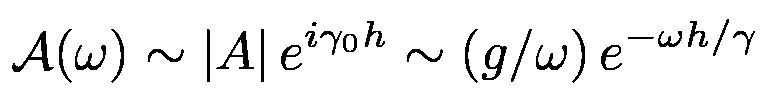
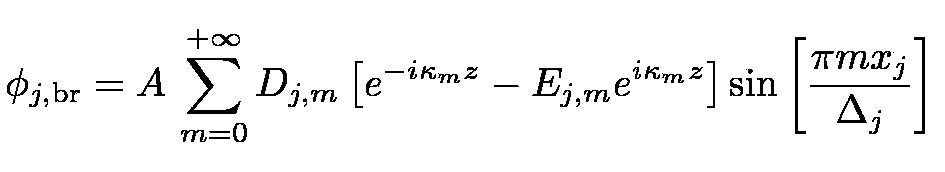
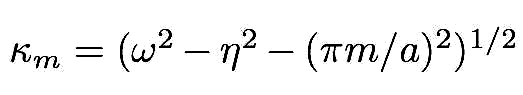 and
and 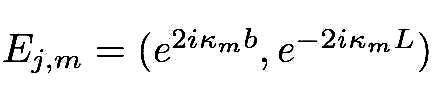 ,
xj = (x, x-a) and Δj = (a, l-a) in the intervals x∈[0, a]
(j = 1) and x∈[a, l] (j = 2), respectively. Choosing Dirichlet boundary conditions, the amplitudes of the propagating waves
satisfy the system of linear inhomogeneous algebraic equations:
,
xj = (x, x-a) and Δj = (a, l-a) in the intervals x∈[0, a]
(j = 1) and x∈[a, l] (j = 2), respectively. Choosing Dirichlet boundary conditions, the amplitudes of the propagating waves
satisfy the system of linear inhomogeneous algebraic equations:
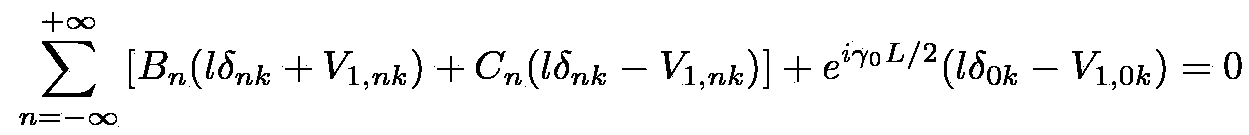
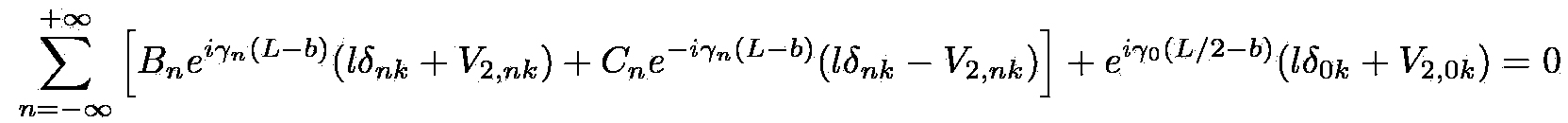
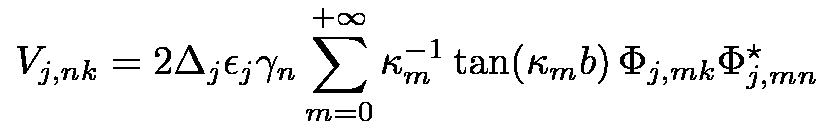
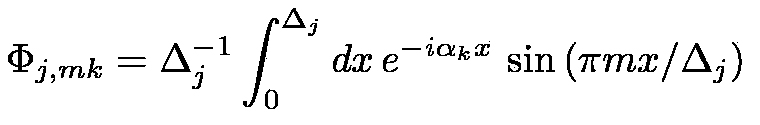
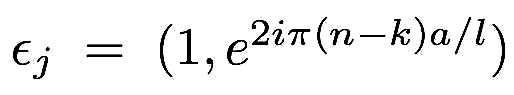 . The power emitted in the bulk follows from Eq.
(3) after solving Eqs. (12) for the propagating wave amplitudes Bn and
Cn. Generalizing to D spacetime dimensions and taking the relativistic limit, we
have
. The power emitted in the bulk follows from Eq.
(3) after solving Eqs. (12) for the propagating wave amplitudes Bn and
Cn. Generalizing to D spacetime dimensions and taking the relativistic limit, we
have
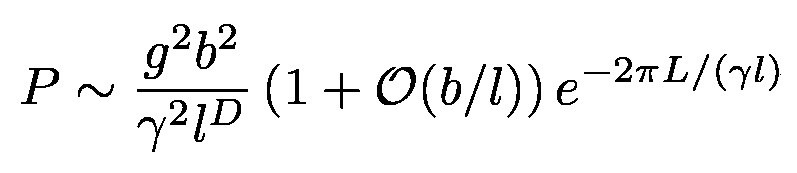
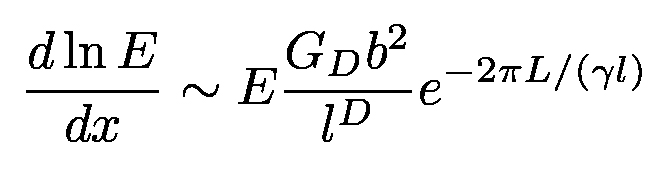
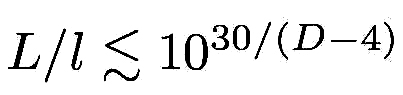 and
and 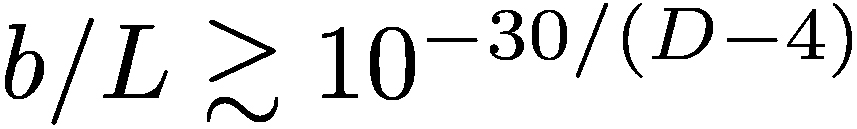 . The largest γ factors are
observed in ultra high-energy cosmic rays, reaching 1011
. The largest γ factors are
observed in ultra high-energy cosmic rays, reaching 1011